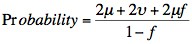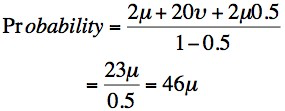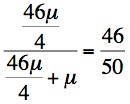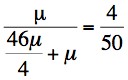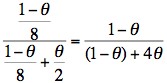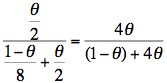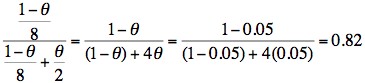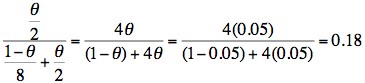Introduction
Risk assessment is an essential part of genetic counselling and much of this is based upon Bayesian risk analysis. Bayesian analysis is a method of combining probabilities and which is used to calculate the probability of having or not having a disease causing mutation after a negative test is obtained. Bayesian analysis is derived from ‘An Essay Toward Solving a Problem in the Doctrine of Chances' by the Reverend Thomas Bayes and published posthumously in 1763.
In X-linked disorders, risk analysis is generally undertaken for 2 reasons:
1.
A male with Haemophilia exists within a family and the female members in that kindred wish to establish whether they are haemophilia carriers or not.
2.
A female with no family history of a bleeding disorder gives birth to a boy with Haemophilia and wishes to know if she is a carrier and therefore, at risk of having similarly affected children. Other females within that family may also wish to know if there are carriers.
Risk assessment is undertaken by an analysis of:
- the Pedigree
- the Phenotype
- the Genotype
- and by combining these it may be possible to establish the probability of carriership in an 'at risk' female. The aim is to establish definitively whether an 'at-risk' female is a carrier or not. However, as you will see this is not always possible.
Principles
1. Pedigree Analysis
An accurate family pedigree forms an essential part of the initial investigation of any family with a bleeding disorder. On the basis of the family pedigree a female may be ‘classified’ as an obligate carrier, a potential carrier or a non-carrier. Risk analysis has to assume correct paternity. Historically the risk of non-paternity has been estimated to be as high as 10% but more recent data suggests that it is in the region of 1.9%.
For Guidelines on pedigree drawing and recommendations for standardised Human pedigree nomenclature - see References. Various packages are available for drawing family pedigrees - see References
Obligate Carriers of X-Linked Recessive Disorders
In haemophilia A or B, the four pedigrees below illustrate the concept of obligate carriership i.e. a female must be a carrier of the abnormal F8 or F9 gene from the pedigree. This assumes correct paternity.
| Pedigree | Interpretation |
|---|---|
| Pedigree 1 | The daughters [II:3] of a male with Haemophilia A or B [or other X-linked disorder] are obligate carriers - in this case II:3 - as they must inherit the affected X-chromosome from their biological father. |
| Pedigree 2 | A woman (I:2) with two sons [II:1 and II:2] that both have Haemophilia. |
| Pedigree 3 | A mother with a single son with Haemophilia but from a family in which there is a history of Haemophilia. |
| Pedigree 4 | II:2 and II:4 are obligate carriers as they are sisters each with a son that has Haemophilia. |
Bayesian Analysis Using Pedigree Data:
Pedigree 5
Let us now the consider the pedigree shown below - Pedigree 5:
I:2 has 2 sons with (in this pedigree) severe Haemophilia A (VIII:C<1 IU/dL) - and she is, therefore, an obligate carrier of severe Haemophilia A. She has a daughter II:3 who wishes to know if she is a carrier or not.

We can use Bayesian risk analysis to establish the risk that II:3 is or is not a carrier of severe Haemophilia A. We are assuming that F8 mutational analysis is not available or that this is one of the families, approximately 3-4% of cases, in which no mutation can be identified within the F8 gene.
So - Bayes theorem or law states:
1. If the prior probability of an event C occurring is denoted as P(C) and
2. the prior probability an event C not occurring is denoted as P(NC) and
3. the conditional probability of an observation O occurring if C occurs is P(O/C) and
4. the conditional probability of an observation O occurring if C does not occur is P(O/NC)
5. then the overall probability of event C given O, equals:
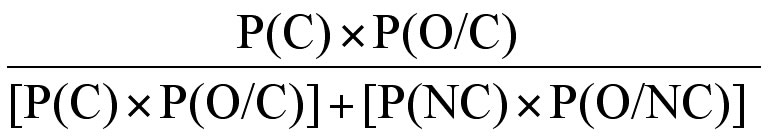
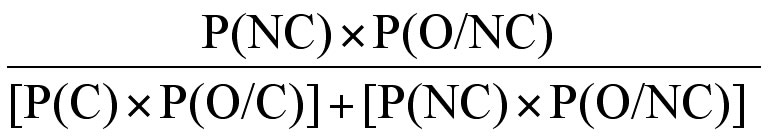
We can use this information in Pedigree 5 to establish the risk that II-3 is or is not a carrier of Haemophilia A. Bayesian analysis usually starts with mutually exclusive hypotheses – in this case whether II:3 is a carrier of severe Haemophilia A or not. Each hypothesis is set out as a column in a table.
This is summarised in the table below:
| Probability | II:3 is a carrier [Event occurs] |
II:3 is not a carrier [Event does not occur] |
|---|---|---|
| Prior probability | P(C) | P(NC) |
| Conditional probability that O occurs | P(O/C) | P(O/NC) |
| Joint probability | PC x P(O/C) | P(NC) x P(O/NC) |
| Final [or posterior] probability | 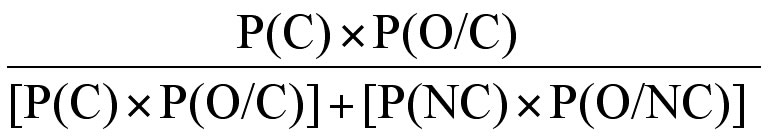 |
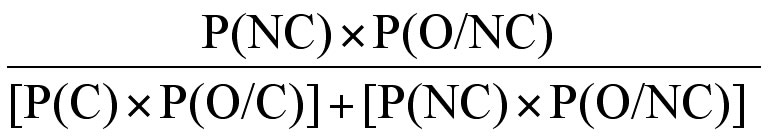 |
The event (C) in this case is whether or not II:3 is a carrier of severe haemophilia and so:
| P(C): P(NC): |
The probability that an event (C) occurs The probability that an event (C) does not occur |
| P(O/C): P(O/NC): |
The conditional probability of observation (O) occurring if event C occurs The conditional probability observation (O) occurring if event C does not occur |
| P(C) x P(O/C): P(NC) x P(O/NC): |
The joint probability of observation (O) occurring if event C occurs The joint probability of observation (O) occurring if event C does not occur |
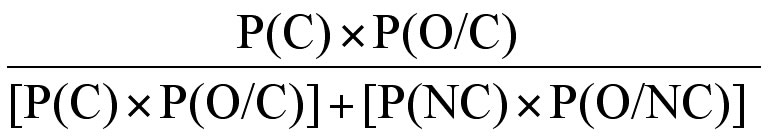 |
The final or posterior probability of observation (O) occurring if event C occurs |
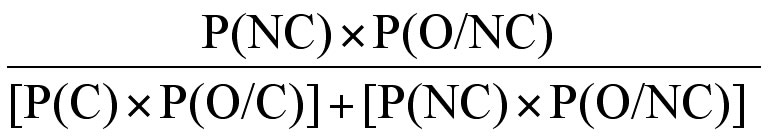 |
The final or posterior probability of observation (O) occurring if event C does not occur |
It is simpler to see how this works if we make the substitutions in the table taking into account the pedigree data from Pedigree 5: So -
Probability II:3 is a carrier
[Event occurs]II:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs 1 ~1 Joint probability 1/2 1/2 Final [or posterior] probability 1/2
--------------
1/2 + 1/2
= 1/21/2
--------------
1/2 + 1/2
= 1/2
Prior Probability:
1. The prior probability of II:3 being a carrier is 1/2 as she has a 1/2 chance of inheriting the abnormal X-chromosome from her mother that carries the F8 gene mutation.
2. The risk of II:3 not being a carrier is also 1/2 as she has a 1/2 chance of inheriting the normal X-chromosome from her mother that does not carry the F8 gene mutation.
Conditional Probability:
1. The conditional probability that II:3 is a carrier if she inherits the X-chromosome from her mother that carries the abnormal F8 gene is 1 i.e. she must be a carrier if she inherits the abnormal F8 gene.
2. The conditional probability that II:3 is a not carrier if she does not inherit the X-chromosome from her mother that carries the abnormal F8 gene is almost 1 i.e. she cannot be a carrier if she does not inherit the abnormal F8 gene but she could develop a new mutation in her F8 gene. If II:3 is not a carrier the conditional probability that a son would be normal is [1-µ] where µ is the F8 gene mutation rate in females. This is an extremely small risk [in the region of 1/10,000] and to simplify the calculations this has been ignored this and we have assumed the probability is ~1.
Joint Probability:
1. The joint probability of observation (O) occurring if event C occurs takes into account both the prior probability and the conditional probability and is derived by multiplying the two events e.g. 1/2 x 1 = 1/2.
2. Similarly the joint probability of observation (O) occurring if event C does not occur takes into account both the prior probability and the conditional probability and is derived by multiplying the two events e.g. 1/2 x 1 = 1/2.
Final [or posterior] Probability
1. The final or posterior probability of observation (O) occurring if event C occurs is derived from the joint probability (1/2) divided by the sum of the joint probabilities (1/2 + 1/2 = 1) = 1/2.
2. Similarly the final or posterior probability of observation (O) occurring if event C does not occur is derived from the joint probability (1/2) divided by the sum of the joint probabilities (1/2 + 1/2 = 1) = 1/2.[Note: The sum of the final of observation (O) occurring if event C occurs and the final or posterior probability of observation (O) occurring if event C does not occur is always 1.]
So in this case - Bayesian analysis provides us with no additional information on the risk that II:3 is or is not a carrier. Our calculations show that the risk of II:3 being a carrier is 1/2 and of not being a carrier is also 1/2.
Bayesian Analysis Using Pedigrees with Additional Data:
Pedigree 6aConsider the pedigree (Pedigree 6A) shown below in which there are several males with severe haemophilia A [VIII:C <1 IU/dL]. This is similar to Pedigree 5 but with additional family members:
II:2 has 2 sons with (in this pedigree) severe Haemophilia A (VIII:C<1 IU/dl) and a brother with severe Haemophilia A - she is, therefore, an obligate carrier of severe Haemophilia A (see definitions of obligate carriers above). She has a daughter III:3 who wishes to know if she is a carrier of severe Haemophilia A or not.
III:3 already has two sons who do not have Haemophilia A. We can use this additional data i.e. the fact that III:3 has two sons without Haemophilia A, in a Bayesian risk analysis to establish the risks that III:3 is or is not a carrier. So...
Probability III:3 is a carrier
[Event occurs]III:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs 1/2 x 1/2 = 1/4 ~1 Joint probability 1/2 x 1/4 = 1/8 1/2 x 1 = 1/2 Final [or posterior] probability 1/8
----------
1/8 + 1/2
= 1/51/2
----------
1/8 + 1/2
= 4/5
1. Prior Probability: So – in the pedigree above (and the table) – the prior probability [P(C)] that III:3 is a carrier of severe haemophilia A is 1/2 and the prior probability that she is not a carrier [P(NC)] of severe haemophilia A is also 1/2. [III:3 has a 1/2 chance of inheriting or not inheriting the abnormal X-chromosome from her mother that carries the F8 gene mutation depending on which of the two X-chromosomes she inherits.]2. Conditional Probability: III:3 has 2 normal sons.
If III:3 is a carrier then the conditional probability that both would be 'normal' i.e. do not have severe Haemophilia A, is 1/2 x 1/2 = 1/4. [Each son of III:3 has a 1/2 chance, if their mother is a carrier, of having severe Haemophilia A.]
If she is not a carrier then the conditional probability that both sons would be 'normal' is almost 1. It is not exactly 1 because there is a risk that a son could have Haemophilia A because of a new, spontaneous mutation.3. Joint Probability: The joint probability that III:3 is a carrier [P(C) x P(O/C)] is: 1/2 x 1/4 = 1/8 and the joint probability that III:3 is not a carrier [P(NC) x P(O/NC)] is: 1/2 x 1 = 1/2.
Any observation that modifies this prior probability allows conditional probabilities to be established for each hypothesis using posterior information such as the results of carrier detection studies or in the pedigree described – the finding that III:3 has two boys without Haemophilia A. The conditional probabilities are the probabilities that III:3 would have 2 unaffected sons if she was a carrier or not a carrier. The resulting probability for each is known as the joint probability and is derived from multiplying the prior probability by the conditional probability.
4. The Final [or Posterior] Probability: The overall final probability for each event is known as the posterior or relative probability and is obtained by dividing the joint probability by the sum of all the joint probabilities. This ensures that the sum of all the posterior probabilities will equal 1.
So in this pedigree - the risk the III:3 is a carrier of severe haemophilia A is 1/2 based solely on the finding that her mother is an obligate carrier but this probability changes to 1/5 that she is a carrier and 4/5 that she is not a carrier if we take into account the fact that she has had two unaffected sons.
Pedigree 6B
If III:3 was to have another son without haemophilia - this would further reduce the risk that she is a carrier.
Probability III:3 is a carrier
[Event occurs]III:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs 1/2 x 1/2 x 1/2 = 1/8 ~1 Joint probability 1/2 x 1/8 = 1/16 1/2 x 1 = 1/2 Final [or posterior] probability 1/16
----------
1/16 + 1/2
= 1/91/2
----------
1/16 + 1/2
= 8/9
The risk, therefore, that III:3 is a carrier if she has three boys without Haemophilia A, is 1/9 and the risk that she is not a carrier is 8/9. This demonstrates that the pedigree data can significantly alter the probability that someone is or is not a carrier.
Bayesian Analysis in families in which there is only a single male with Haemophilia:
Pedigree 7aBayesian analysis can be used to assess carrier risk in families in which there is only a single affected male. In the pedigree below, I-2 has a son (II:1) with severe haemophilia B and a daughter (II:2). II-2 wishes to establish her carrier status.
The probability that any female is a carrier can be derived from the formula:
- where µ is the mutation rate in females, v is the mutation rate in males and f is the biological fitness i.e. the ability to reproduce and have healthy children. f can vary between 0 - a lethal mutation [as is the case with some X-linked disorders] and 1 - the normal allele. A biological fitness of 0.5 implies that these males have only half as many children as their unaffected male siblings or healthy males in the general population.
In haemophilia the biological fitness of males (f) with Haemophilia A has been estimated to lie between 0.3 – 0.7 (but may be greater in the 21st century because of effective replacement therapy).
The mutation rate in male gametes (v) is estimated at about 10X that of female gametes (µ). This is because of the greater number of cell divisions that cells undergo during meiosis and the formation of males gametes compared to female gametes ]Therefore – if we assume for the above pedigree that f = 0.5 and v = 10, then the prior probability of a female being a carrier is:
- where µ is the mutation rate in females. So there is a prior probability of 46µ that any female is a carrier. This assumes that the biological fitness is not zero (0) and that there is a difference in mutation rates between females and males. If the biological fitness is zero and there is no difference in the mutation rates between male and female gametes then the formula simplifies to 4µ.
In order to derive the risk that II:2 is a carrier in Pedigree 7a, the risk for I:2 must be calculated:
Probability I:2 is a carrier
[Event occurs]I:2 is not a carrier
[Event does not occur]Prior 46µ 1-46µ Conditional probability that O occurs 1/2 µ Joint probability 46µ x 1/2 = 23µ 1 x µ = µ Final [or posterior] probability 23µ
----------
23µ + µ
= 23/2423µ
----------
23µ + µ
= 1/24
So - from the pedigree and taking into account both the biological fitness and the difference in mutation rates between male and female gametes, I:2 is highly likely to be a carrier of Haemophilia A [23/23 = 95%). This is confirmed by a number of studies that have shown that in families with a single male with Haemophilia, the mother is a carrier in about 85-90% cases.We can now use this data to establish the risk that II:3 is a carrier or not. The risk that she is a carrier of severe Haemophilia A is 23/24 x 1/2 =22/48.
Pedigree 7b
Let us now consider the case of Pedigree 7b. This is similar to Pedigree 7a but with additional family members:
In the pedigree below, I-2 has a son (II:1) with severe Haemophilia A, a boy without Haemophilia A and a daughter (II:3). II-3 has two boys without Haemophilia A but wishes to establish her carrier status. We start again by establishing the probability I:2 is or is not a carrier:
Probability I:2 is a carrier
[Event occurs]I:2 is not a carrier
[Event does not occur]Prior 46µ 1-46µ Conditional probability that O occurs
1 son with Haemophilia A
I son without Haemophilia A
1/2
1/2
µ
1Joint probability 46µ x 1/2 x 1/2 = 46µ/4 1 x µ x 1= µ Final [or posterior] probability
So we now use this data to establish the risk that II:3 is a carrier taking into account that she also has 2 sons without Haemophilia A. So -
Probability I:2 is a carrier I:2 is not a carrier II:3 Prior Conditional probability of
2 sons without Haemophilia AJoint probability Final [or posterior] probability
So - If I:2 is a carrier, the probability that II:2 is not a carrier is 176/230 = 76.5%.
If I:2 is not a carrier, the probability that II:2 is not a carrier is 4/5 = 80%.
2 & 3. Incorporating Phenotypic and Genotypic Data into Bayesian Risk Calculations
We can increase the complexity of these calculations [considerably] by adding in additional phenotypic data [e.g. the results of FVIII & VWF:Ag assays] and genotypic data [e.g. the results of genetic linkage studies.]
A. Phenotypic (coagulation) Data: In the following pedigree [Pedigree 6A] with severe Haemophilia A, II:3 wishes to establish her carrier status and her risk of having children with severe haemophilia A.
If we have no other data available other than the pedigree, then the risks that III:3 is or is not a carrier is shown below:
Probability II:3 is a carrier
[Event occurs]II:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs 1/2 x 1/2 = 1/4 ~1 Joint probability 1/2 x 1/4 = 1/8 1/2 x 1 = 1/2 Final [or posterior] probability 1/8
----------
1/8 + 1/2
= 1/51/2
----------
1/8 + 1/2
= 4/5
If we now obtain the results of Factor assays [VIII:C and VWF:Ag data] and these show a VIII:C/VWF:Ag ratio of 0.63. From previous measurements of VIII:C and VWF:Ag and a calculation of the VIII:C/VWF:Ag ratio in a cohort of obligate carriers of Haemophilia A and of normal women, 3/4 obligate carriers were found to have an VIII:C/VWF:Ag ratio <0.65 but only 1/16 women who were not carriers of Haemophilia A.
If we incorporate this additional phenotypic data data into our risk analysis table, then:
Probability II:3 is a carrier
[Event occurs]II:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs
2 normal sons
VIII:C/VWF:Ag ratio = 0.63
1/2 x 1/2 = 1/4
3/4
~1
1/16Joint probability 1/2 x 1/4 x 3/4 = 3/32 1/2 x 1 x 1/16 =1/32 Final [or posterior] probability 3/32
---------------
3/32 + 1/32
= 3/41/32
---------------
3/32 + 1/32
= 1/4
So we can see that the phenotypic data has completely changed the probability that II:3 is a carrier [from 1/5 to 3/4]. Additional data such as genotypic data might further alter this risk.To take this a step further - what happens if the phenotypic data is reversed i.e. the VIII:C/VWF:Ag Ratio = 0.72.
If we make the substitutions in the risk table:
Probability II:3 is a carrier
[Event occurs]II:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs
2 normal sons
VIII:C/VWF:Ag ratio = 0.63
1/2 x 1/2 = 1/4
1/16
~1
3/4Joint probability 1/2 x 1/4 x 1/6 = 1/128 1/2 x 1 x 3/4 =3/8 Final [or posterior] probability 1/128
---------------
1/128 + 3/8
= 1/493/8
---------------
1/128 + 3/8
= 48/49So - in this case the phenotypic data has significantly changed the chances that II:3 is a carrier.
B. Genotypic Data: In the following pedigree [Pedigree 8] with severe haemophilia A, linkage analysis was used to track the abnormal F8 gene within a family. Mutation data was not available. The family was informative for only a single, extragenic polymorphism [Bgl II] which is closely linked to the F8 gene locus but not part of it. There is a 5% chance of recombination taking place using this linked marker.
The section on Linkage Analysis explains this in more detail.
Analysis of the pedigree shows that the haemophilic F8 gene is linked to the 5.8kb allele and that III:3 has inherited this from her mother II:1. However as this is a linked marker - there is a 5% chance of recombination taking place and therefore a 5% chance that our assumption that she [II:3] is a carrier is incorrect. Measuring her FVIII:C/vWF:Ag ratio may be of value but in this case was 0.78 i.e. normal.
The recombination fraction (θ) is an estimate of the likelihood of recombination taking place. In this case - the recombination fraction (θ) is 5% (0.05.) So - if we construct our risk calculation table as before:
Probability II:3 is a carrier
[Event occurs]II:3 is not a carrier
[Event does not occur]Prior probability 1/2 1/2 Conditional probability that O occurs
2 normal sons
Bgl II linkage data
1/2 x 1/2 = 1/4
1-θ
~1
θJoint probability 1/2 x 1/4 x (1-θ) = (1-θ)/8 1/2 x 1 x θ = θ/2 Final [or posterior] probability
Remember θ is the recombination fraction and using this linked extragenic marker, the risk of recombination is 5% (0.05.) So - if we substitute 0.05 for θ then the risk of II:3 being a carrier is:
and the risk of II:3 not being a carrier is:
This family is interesting in that II:3 has inherited the same allele (5.8kb) as the males that have haemophilia and which strongly suggests that she is a carrier. However, Bayesian risk analysis takes into account both the 5% chance of recombination using this linked extragenic marker and that the fact that II:3 has had two boys without haemophilia.
In practice due to the risk of recombination using linked extragenic markers, assignment of carriership should use intragenic markers and if these are not available a number [i.e. at least 2] of extragenic makers closely linked to the gene under study should be used. .
What Test Next
The next tests would include:
a. Factor assays
b. Some form of genetic testing which is commonly mutation analysis but may include linkage analysis in some families in which no mutation can be identified (approximately 4% of families) or if mutation analysis is not available.
Click HERE to return to the top of the page.